트리에 대해 알아보자.
트리 Tree
트리는 이름처럼 나무를 거꾸로 뒤집어 놓은 형태로 가장 위 Root부터 아래로 뻗어 내려가는 단방향 그래프입니다.
두 노드 사이의 하나의 간선만 연결되어 있는 형태이며, 하나의 노드에 여러 개의 노드가 연결될 수 있는 비선형 자료구조입니다.
트리의 가장 큰 특징은 루트노드를 제외한 모든 노드는 단 하나의 부모노드를 가진다는 것 입니다.
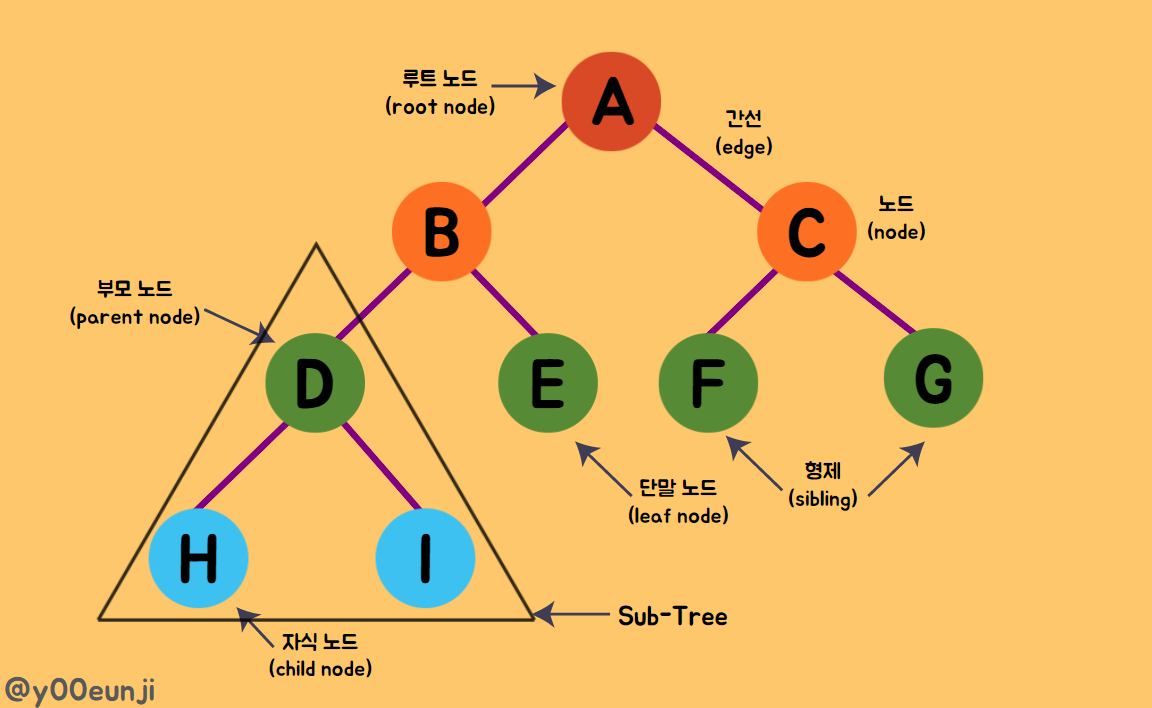
트리 용어
- 노드 Node : 트리에서 데이터를 저장하는 기본적인 단위
간선 edge : 두 노드간의 연결을 나타내는 연결선
루트 Root : 트리 구조에서 최상위 노드
부모 노드 Parent node : 특정 Sub-Tree 내에서의 상위 노드
자식 노드 Child node : 특정 Sub-Tree 내에서의 하위 노드
단말 노드 Leaf Node : 트리 구조의 끝 지점이며 자식 노드가 없는 노드
- 형제 노드 sibling Node : 같은 부모 노드를 갖는 노드
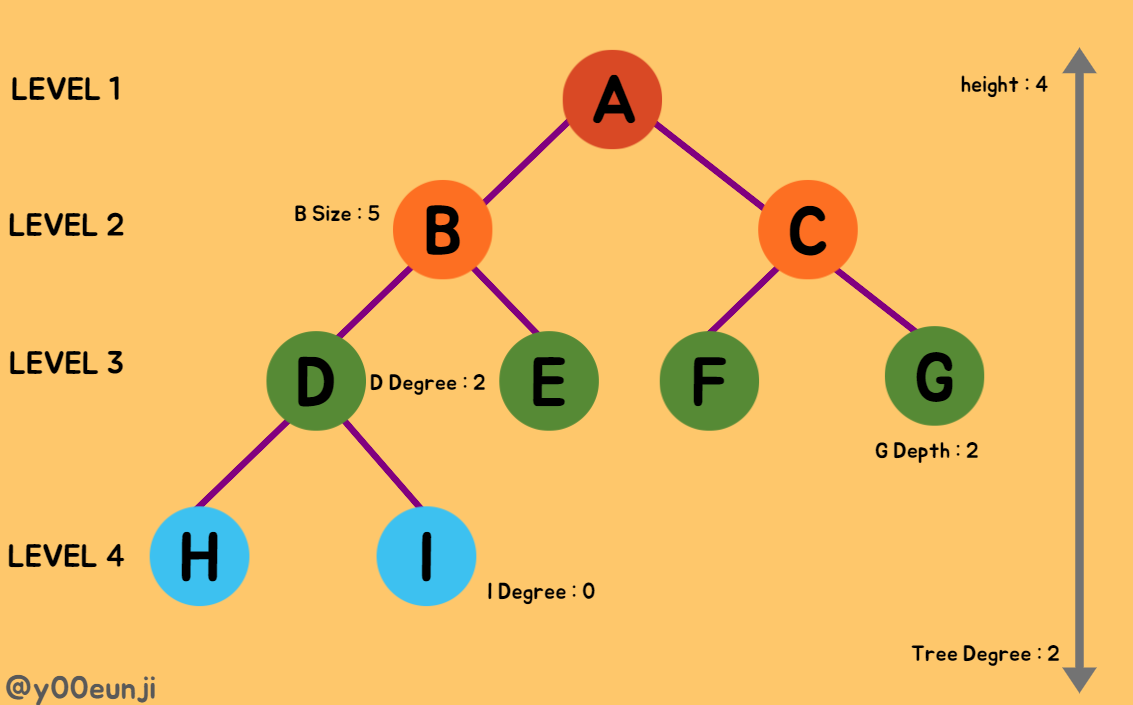
트리 정보
깊이 Depth : 루트에서 특정 노드에 도달하기 위한 간선의 개수
크기 Size : 자신을 포함한 모든 자손의 노드 개수
레벨 Level : 트리의 특정 깊이를 가지는 노드의 집합
차수 Degree : 노드가 지닌 간선의 수
트리 차수 Degree of Tree : 트리의 최대 차수
트리 높이 Height : 트리의 최대 깊이
이진 트리 Binary Tree
자식 노드의 갯수가 2개 이하인 트리를 말합니다.
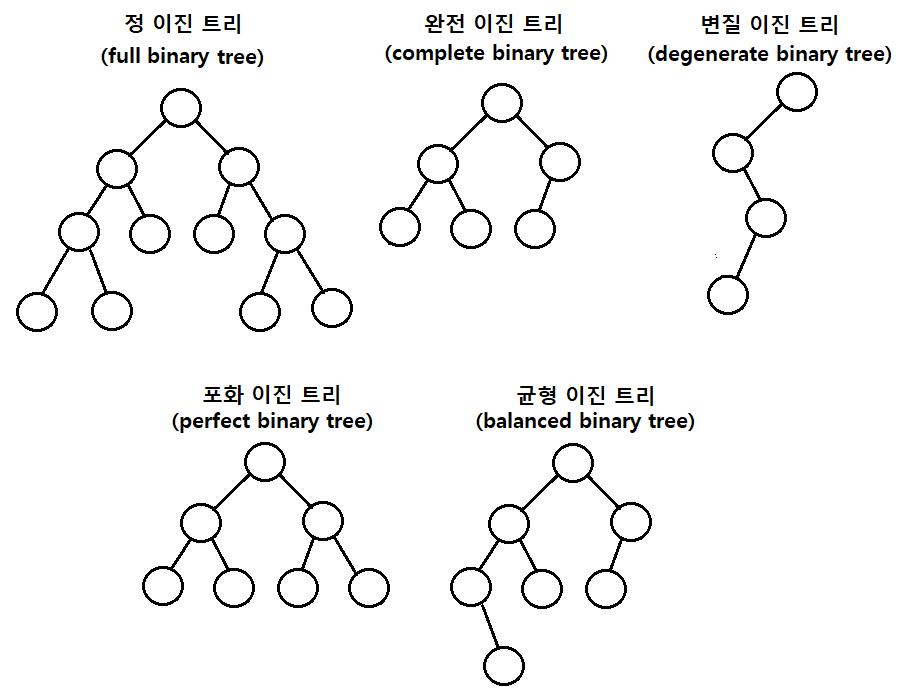
정 이진 트리 Full binary tree
자식 노드가 0 또는 2개인 이진 트리
노드의 개수 <= 2^(h+1)-1 (h = 높이)
완전 이진 트리 Complete binary tree
왼쪽에서부터 채워져 있는 이진 트리
노드의 개수 < 2^(h+1)-1 (h = 높이)
변질 이진 트리 Skewed binary tree
자식 노드가 하나밖에 없는 이진 트리
노드의 개수 = h (h = 높이)
포화 이진 트리 Perfect binary tree
모든 노드가 꽉 차 있는 이진 트리
노드의 개수 = 2^(h+1)-1 (h = 높이)
균형 이진 트리 Balanced binary tree
왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리
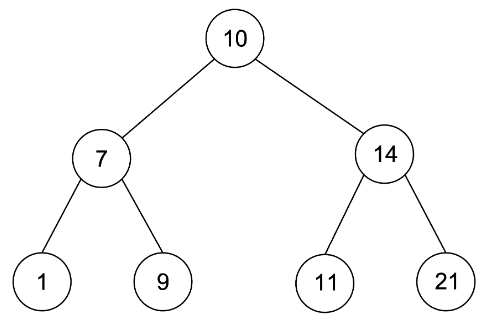
이진 탐색 트리 Binary Search Tree
이진 탐색이 동작할 수 있도록 고안된 자료구조입니다.
이진 탐색트리에서 노드의 값이 저장되는 규칙
- Left Node에는 부모 노드보다 작은 값이 저장
- Right Node에는 부모 노드보다 큰 값이 저장
- 모든 노드 중복 X
이진 탐색 트리의 추상 자료형 ADT
- add : 데이터를 이진 탐색 트리 규칙에 맞는 위치에 추가
- remove : 데이터가 있다면 삭제
- lockUp : 데이터가 있다면 출력
구현 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
add(value) {
let newNode = new Node(value);
if (this.root == null) {
this.root = newNode;
} else {
let curNode = this.root;
while (true) {
if (curNode.value > value) {
if (curNode.left) {
curNode = curNode.left;
} else {
curNode.left = newNode;
break;
}
} else if (curNode.value < value) {
if (curNode.right) {
curNode = curNode.right;
} else {
curNode.right = newNode;
break;
}
} else {
break;
}
}
}
}
remove(value) {
let curNode = this.root;
let parentNode = null;
while (curNode) {
if (curNode.value > value) {
parentNode = curNode;
curNode = curNode.left;
} else if (curNode.value < value) {
parentNode = curNode;
curNode = curNode.right;
} else {
if (curNode.right) {
if (curNode.left) {
// 삭제할 노드의 자식노드가 둘다 존재 하는 경우
// left에서 가장 큰 수로 대체
let maxNode = curNode.left;
let maxNodeParent = null;
// 가장 큰 수 찾기
while (maxNode.right) {
maxNodeParent = maxNode;
maxNode = maxNode.right;
}
// 삭제 할 노드의 부모 노드와 연결
if (parentNode.value > maxNode.value) {
parentNode.left = maxNode;
} else {
parentNode.right = maxNode;
}
maxNode.right = curNode.right;
// 노드 대체로 꼬인 형제 노드 정리
if (maxNodeParent) {
maxNodeParent.right = maxNode.left;
maxNode.left = maxNodeParent;
}
} else {
// 삭제할 노드의 자식노드가 right만 존재 하는 경우
// 삭제할 노드의 right로 대체
// 삭제 할 노드의 부모 노드와 연결
if (parentNode.value > curNode.right.value) {
parentNode.left = curNode.right;
} else {
parentNode.right = curNode.right;
}
}
} else {
if (curNode.left) {
// 삭제할 노드의 자식노드가 left만 존재 하는 경우
// 삭제할 노드의 left로 대체
// 삭제 할 노드의 부모 노드와 연결
if (parentNode.value > curNode.left.value) {
parentNode.left = curNode.left;
} else {
parentNode.right = curNode.left;
}
} else {
// 삭제 할 노드의 자식 노드가 없는 경우
if (parentNode.value > curNode.value) {
parentNode.left = null;
} else {
parentNode.right = null;
}
}
}
return curNode;
}
}
lockUp(value) {
if (this.root == null) return false;
let curNode = this.root;
while (curNode !== null) {
if (curNode.value > value) {
curNode = curNode.left;
} else if (curNode.value < value) {
curNode = curNode.right;
} else {
return curNode;
}
}
}
}
}