알고리즘이 얼마나 효율적인지 알아보자.
- 실행 시간과 사용된 메모리 관점에서 알고리즘 구현을 분석해보자.
시간 복잡도 & 수행 시간
시간 복잡도
주어진 문제를 해결하기 위한 연산 횟수를 말합니다.
수행 시간
1억 번의 연산을 1초로 생각하여 계산한 시간
시간 복잡도 유형
- 빅-오메가 : 최선일 때의 연산 횟수 (Best case)
- 빅-세타 : 보통일 때의 연산 횟수 (Average case)
- 빅-오 : 최악일 때의 연산 횟수 (Worst case)
0 ~ 99 사이의 임의의 숫자를 맞추는 로직
빅-오메가 : 1번, 빅-세타 : n/2번, 빅-오 : n번
빅-오 (Big-O)
알고리즘의 성능을 수학적으로 표현해주는 표기법입니다.
실제 처리 시간을 표시한 것은 아니지만 알고리즘의 성능을 예측할 때 사용합니다.
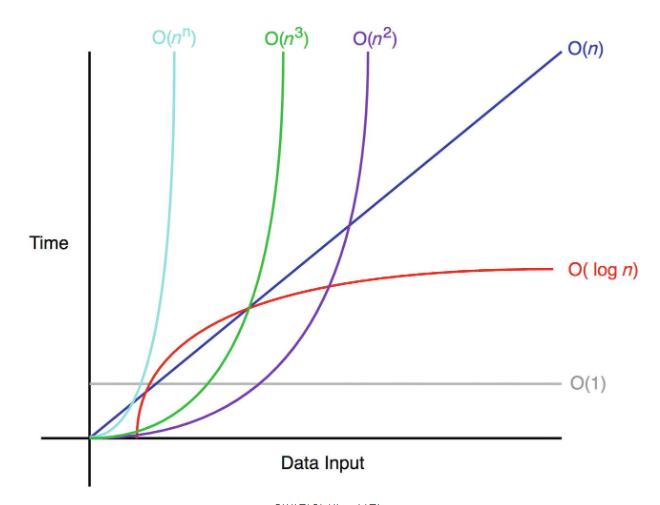
빅-오 종류
O(1) - 상수 시간 (Constant Time)
입력값이 증가하더라도 시간은 일정합니다.
- 예시 : 인덱스로 배열 값 출력 등
O(n) - 선형 시간 (Linear Time)
입력값이 증가함에 따라 시간이 같은 비율로 증가합니다.
- 예시 : 0 ~ n-1 의 숫자를 출력 등
O(n^2) - 2차 시간 (Quadratic Time)
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가합니다.
O(2^n)
입력값이 1 증가함에 따라 시간이 2배로 증가합니다.
O(log n)
한번 연산할 때 마다 n이 1/2 줄어듭니다.
O(1) 다음으로 빠른 시간 복잡도이며,
빅-오 계산 규칙
항상 최악의 상황을 계산
계수, 상수 제거
O(k * n) = O(n), O(n + 1) = O(n)
합의 법칙
O(a) + O(b) = O(a + b)
곱의 법칙
O(a) x O(b) = O(a x b)
입력 데이터로 시간 복잡도 예측
1초 기준 입력 데이터 크기에 따른 시간 복잡도
- n <= 1,000,000 : O(n) / O(log n)
- n <= 10,000 : O(n^2)
- n <= 500 : O(n^3)